Een ratio wil wat zeggen over de verhoudingen van objecten die je in het dagelijks leven gebruikt. Een vierkant heeft een verhouding van 1:1 omdat beide zijdes gelijk zijn, een rechthoek kan bijvoorbeeld een ratio hebben van 2:1. De verhouding 2:1 betekend dat de ene zijde twee keer zo lang is als de andere zijde.

Fabricage gedreven ratio’s

We komen overal ratio’s tegen, dit komt omdat we in een gestandaardiseerde wereld leven waar fabrikanten erg veel baat hebben bij standaard ratio’s. Normale televisie beelden worden afgespeeld op je televisie met een verhouding van 16 units breed en 9 units hoog (dus 16:9) de televisie fabrikant wil natuurlijk niet dat je zwarte balken aan de boven/onderkant of zijkanten ziet en maakt dus waarschijnlijk jouw televisie ook in die verhouding. Echter wanneer je een film afspeelt dan heeft deze vaak de verhouding 21:9 (breedbeeld) en krijg je dus wel balken boven en onder te zien.

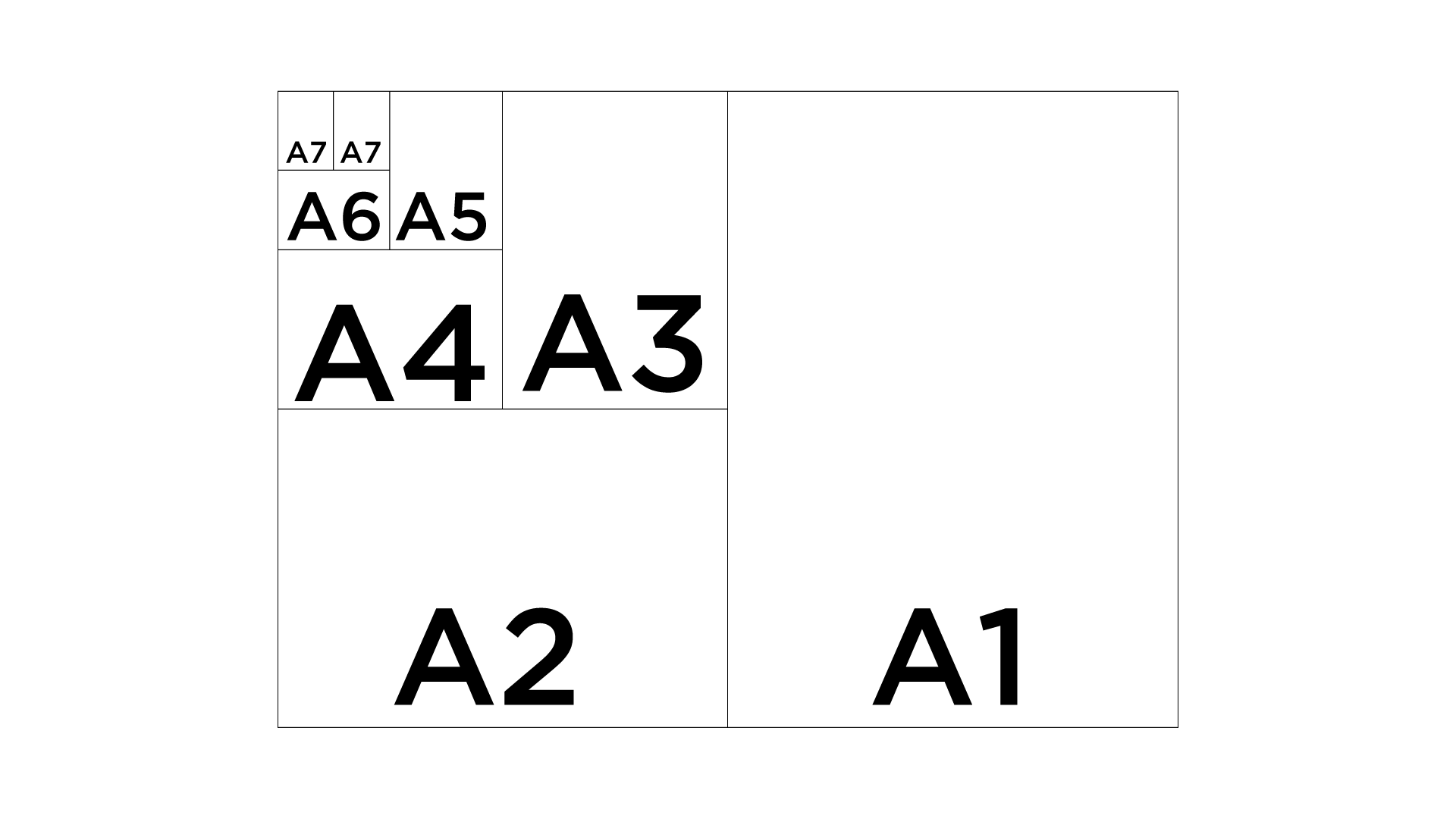
Waar je ook een verhouding tegen komt als praktisch formaat is bijvoorbeeld je A4 papier vanuit je printer. Een A4 papier is twee keer zo groot als een A5 papier, een A5 papier is twee keer zo groot als een A6 papier.

Alle verhoudingen van papier is vast gezet met een ISO norm en het maakt dus niet uit waar ter wereld je een papier koopt, het heeft overal de zelfde verhouding en formaat. (De A-serie is wat wij hier in Nederland het meest gebruiken.)         De A-serie papier begint bij A0 en loopt tot A10, een A0 papier heeft het formaat van 1189mm x 841mm wat precies een één vierkante meter is. De aspect ratio van A-series papier is a/b = √2 en dat is ongeveer een verhouding van 1:141421…

Natuur gedreven ratio

Niet alleen de mensen zijn er achter gekomen dat bepaalde ratio’s erg handig kunnen werken want de natuur is ons als miljoenen jaar voor geweest. Sommige lezers weten misschien al waar ik over ga schrijven; de Fibonacci sequence.

Fibobacci sequence

De verhouding werd door beroemd gemaakt door Leonardo of Pisa later bekend als Fibonacci in het boek Liber Abaci in het jaar 1202. In dit boek werd een volgorde beschreven over hoe konijnen zich voor voort plantte in een veld.

De volgorde van dit alles komt overal terug in de natuur, de volgorde van de Fibonacci reeks is als volgt:
1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987 et cetera. Het komende getal is de som van de twee laatste getallen. Dus als je de reeks 1, 1, 2, 3, 5, hebt gehad dan tel je 3 + 5 en krijg je 8.

Wanneer je deze hele reeks door rekent dan komt daar natuurlijk ook een verhouding uit, het is de verhouding 1 op 0.618…. of 1.618…

Hier zie je het bij een voorbeeld van een zonnebloem, de zaadjes van de zonnebloem zijn verdeeld door middel van de Fibonacci volgorde. Iedere 360 graden(cirkel) * 0.618 (Fibonacci ratio) zit een zaadje.
Op deze manier kan de bloem het maximaal aantal zaadjes kwijt en daarbij zo compact mogelijk blijven.

Ontwerp gedreven ratio’s

Wanneer je een product ontwerpt dan heb je vaak met een stukje vrijheid om bijvoorbeeld te bepalen waar de interface van het product kan komen of welke verhoudingen deze heeft. Natuurlijk gaan praktische zaken zoals functie en ergonomie voor maar wanneer je wat vrijheid hebt dan moet de deze weloverwogen gebruiken om het product nog beter te maken, dit kan namelijk een product naar een hoger niveau tillen zonder dat je daar veel moeite voor hoeft te doen.

De praktische kant van verhoudingen ontwerpen is dat het overal in terug komt, de kootjes van je hand hebben namelijk ook de Fibonacci verhouding dus wanneer je iets vast pakt met deze verhouding voelt het goed aan wat betreft vorm.

Naast dat het fijn voelt lijkt het ook altijd voor het oog te kloppen omdat we zo erg gewend zijn om deze verhouding te zien.

Google

Misschien denk je dat het wel mee zal vallen waar deze verhoudingen allemaal in terug komen, misschien vind je het dan wel de moeite om eens Fibonacci of the golden ratio te zoeken op het internet.

Een aantal voorbeelden kun je vinden op: https://insteading.com/blog/fibonacci-sequence-in-nature/

Wil je meer weten of heb je ergens hulp bij nodig dan kun je altijd vrijblijvend contact opnemen.